\(\renewcommand{\AA}{\text{Å}}\)

8.4.1. CHARMM, AMBER, COMPASS, and DREIDING force fields

A compact summary of the concepts, definitions, and properties of force fields with explicit bonded interactions (like the ones discussed in this HowTo) is given in (Gissinger).

A force field has 2 parts: the formulas that define it and the coefficients used for a particular system. Here we only discuss formulas implemented in LAMMPS that correspond to formulas commonly used in the CHARMM, AMBER, COMPASS, and DREIDING force fields. Setting coefficients is done either from special sections in an input data file via the read_data command or in the input script with commands like pair_coeff or bond_coeff and so on. See the Tools doc page for additional tools that can use CHARMM, AMBER, or Materials Studio generated files to assign force field coefficients and convert their output into LAMMPS input. LAMMPS input scripts can also be generated by charmm-gui.org.

CHARMM and AMBER

The CHARMM force field (MacKerell) and AMBER force field (Cornell) have potential energy function of the form

\[\begin{split}V & = \sum_{bonds} E_b + \sum_{angles} \!E_a + \!\overbrace{\sum_{dihedral} \!\!E_d}^{\substack{ \text{charmm} \\ \text{charmmfsw} }} +\!\!\! \sum_{impropers} \!\!\!E_i \\[.6em] & \quad + \!\!\!\!\!\!\!\!\!\!\underbrace{~\sum_{pairs} \left(E_{LJ}+E_{coul}\right)}_{\substack{ \text{lj/charmm/coul/charmm} \\ \text{lj/charmm/coul/charmm/implicit} \\ \text{lj/charmm/coul/long} \\ \text{lj/charmm/coul/msm} \\ \text{lj/charmmfsw/coul/charmmfsh} \\ \text{lj/charmmfsw/coul/long} }} \!\!\!\!\!\!\!\!+ \!\!\sum_{special}\! E_s + \!\!\!\!\sum_{residues} \!\!\!{\scriptstyle\mathrm{CMAP}(\phi,\psi)}\end{split}\]

The terms are computed by bond styles (relationship between 2 atoms), angle styles (between 3 atoms) , dihedral/improper styles (between 4 atoms), pair styles (non-covalently bonded pair interactions) and special bonds. The CMAP term (see fix cmap command for details) corrects for pairs of dihedral angles (“Correction MAP”) to significantly improve the structural and dynamic properties of proteins in crystalline and solution environments (Brooks). The AMBER force field does not include the CMAP term.

The interaction styles listed below compute force field formulas that are consistent with common options in CHARMM or AMBER. See each command’s documentation for the formula it computes.

The pair styles compute Lennard Jones (LJ) and Coulombic interactions with additional switching or shifting functions that ramp the energy and/or force smoothly to zero between an inner \((a)\) and outer \((b)\) cutoff. The older styles with charmm (not charmmfsw or charmmfsh) in their name compute the LJ and Coulombic interactions with an energy switching function (esw) S(r) which ramps the energy smoothly to zero between the inner and outer cutoff. This can cause irregularities in pairwise forces (due to the discontinuous second derivative of energy at the boundaries of the switching region), which in some cases can result in complications in energy minimization and detectable artifacts in MD simulations.

\[\begin{split}LJ(r) &= 4 \epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6 \right]\\[.6em] C(r) &= \frac{C q_i q_j}{ \epsilon r}\\[.6em] S(r) &= \frac{ \left(b^2 - r^2\right)^2 \left(b^2 + 2r^2 - 3{a^2}\right)} { \left(b^2 - a^2\right)^3 }\\[.6em] E_{LJ}(r) &= \begin{cases} LJ(r), & r \leq a \\ LJ(r) S(r), & a < r \leq b \\ 0, &r > b \end{cases} \\[.6em] E_{coul}(r) &= \begin{cases} C(r), & r \leq a \\ C(r) S(r), & a < r \leq b \\ 0, & r > b \end{cases}\end{split}\]
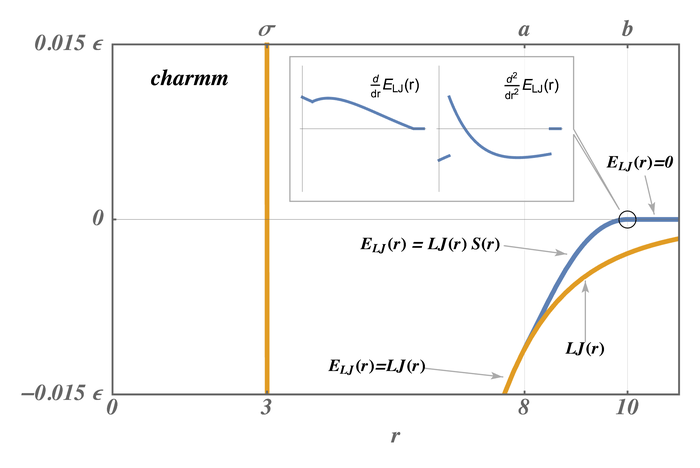
_images/howto_charmm_ELJ.png

The newer styles with charmmfsw or charmmfsh in their name replace energy switching with force switching (fsw) for LJ interactions and force shifting (fsh) functions for Coulombic interactions (Steinbach)

\[\begin{split} E_{LJ}(r) = & \begin{cases} 4 \epsilon \sigma^6 \left(\frac{\displaystyle\sigma ^6-r^6}{\displaystyle r^{12}}-\frac{\displaystyle\sigma ^6}{\displaystyle a^6 b^6}+\frac{\displaystyle 1}{\displaystyle a^3 b^3}\right) & r\leq a \\ \frac{\displaystyle 4 \epsilon \sigma^6 \left(\sigma ^6 \left(b^6-r^6\right)^2-b^3 r^6 \left(a^3+b^3\right) \left(b^3-r^3\right)^2\right)}{\displaystyle b^6 r^{12} \left(b^6-a^6\right)} & a<r \leq b\\ 0, & r>b \end{cases}\\[.6em] E_{coul}(r) & = \begin{cases} C(r) \frac{\displaystyle (b-r)^2}{\displaystyle r b^2}, & r \leq b \\ 0, & r > b \end{cases}\end{split}\]
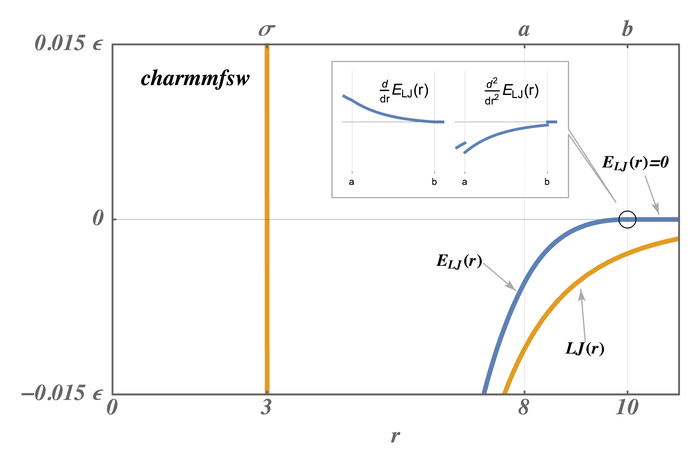
_images/howto_charmmfsw_ELJ.png

These styles are used by LAMMPS input scripts generated by https://charmm-gui.org/ (Brooks).

Note

For CHARMM, newer charmmfsw or charmmfsh styles were released in March 2017. We recommend they be used instead of the older charmm styles. See discussion of the differences on the pair charmm and dihedral charmm doc pages.

Note

The TIP3P water model is strongly recommended for use with the CHARMM force field. In fact, “using the SPC model with CHARMM parameters is a bad idea” and “to enable TIP4P style water in CHARMM, you would have to write a new pair style” . LAMMPS input scripts generated by Solution Builder on https://charmm-gui.org use TIP3P molecules for solvation. Any other water model can and probably will lead to false conclusions.

COMPASS

COMPASS is a general force field for atomistic simulation of common organic molecules, inorganic small molecules, and polymers which was developed using ab initio and empirical parameterization techniques (Sun). See the Tools page for the msi2lmp tool for creating LAMMPS template input and data files from BIOVIA’s Materials Studio files. Please note that the msi2lmp tool is very old and largely unmaintained, so it does not support all features of Materials Studio provided force field files, especially additions during the last decade. You should watch the output carefully and compare results, where possible. See (Sun) for a description of the COMPASS force field.

These interaction styles listed below compute force field formulas that are consistent with the COMPASS force field. See each command’s documentation for the formula it computes.

DREIDING

DREIDING is a generic force field developed by the Goddard group at Caltech and is useful for predicting structures and dynamics of organic, biological and main-group inorganic molecules. The philosophy in DREIDING is to use general force constants and geometry parameters based on simple hybridization considerations, rather than individual force constants and geometric parameters that depend on the particular combinations of atoms involved in the bond, angle, or torsion terms. DREIDING has an explicit hydrogen bond term to describe interactions involving a hydrogen atom on very electronegative atoms (N, O, F). Unlike CHARMM or AMBER, the DREIDING force field has not been parameterized for considering solvents (like water).

See (Mayo) for a description of the DREIDING force field

The interaction styles listed below compute force field formulas that are consistent with the DREIDING force field. See each command’s documentation for the formula it computes.

(Gissinger) J. R. Gissinger, I. Nikiforov, Y. Afshar, B. Waters, M. Choi, D. S. Karls, A. Stukowski, W. Im, H. Heinz, A. Kohlmeyer, and E. B. Tadmor, J Phys Chem B, 128, 3282-3297 (2024).

(MacKerell) MacKerell, Bashford, Bellott, Dunbrack, Evanseck, Field, Fischer, Gao, Guo, Ha, et al (1998). J Phys Chem, 102, 3586 . https://doi.org/10.1021/jp973084f

(Cornell) Cornell, Cieplak, Bayly, Gould, Merz, Ferguson, Spellmeyer, Fox, Caldwell, Kollman (1995). JACS 117, 5179-5197. https://doi.org/10.1021/ja00124a002

(Steinbach) Steinbach, Brooks (1994). J Comput Chem, 15, 667. https://doi.org/10.1002/jcc.540150702

(Brooks) Brooks, et al (2009). J Comput Chem, 30, 1545. https://onlinelibrary.wiley.com/doi/10.1002/jcc.21287

(Sun) Sun (1998). J. Phys. Chem. B, 102, 7338-7364. https://doi.org/10.1021/jp980939v

(Mayo) Mayo, Olfason, Goddard III (1990). J Phys Chem, 94, 8897-8909. https://doi.org/10.1021/j100389a010