\(\renewcommand{\AA}{\text{Å}}\)
pair_style atm command
Syntax
pair_style atm cutoff cutoff_triple
cutoff = cutoff for each pair in 3-body interaction (distance units)
cutoff_triple = additional cutoff applied to product of 3 pairwise distances (distance units)
Examples
pair_style atm 4.5 2.5
pair_coeff * * * 0.072
pair_style hybrid/overlay lj/cut 6.5 atm 4.5 2.5
pair_coeff * * lj/cut 1.0 1.0
pair_coeff 1 1 atm 1 0.064
pair_coeff 1 1 atm 2 0.080
pair_coeff 1 2 atm 2 0.100
pair_coeff 2 2 atm 2 0.125
Description
The atm style computes a 3-body Axilrod-Teller-Muto potential for the energy E of a system of atoms as
where \(\nu\) is the three-body interaction strength. The distances between pairs of atoms \(r_{12}\), \(r_{23}\), \(r_{31}\) and the angles \(\gamma_1\), \(\gamma_2\), \(\gamma_3\) are as shown in this diagram:
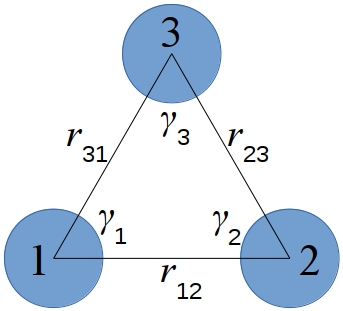
Note that for the interaction between a triplet of atoms \(I,J,K\), there is no “central” atom. The interaction is symmetric with respect to permutation of the three atoms. Thus the \(\nu\) value is the same for all those permutations of the atom types of \(I,J,K\) and needs to be specified only once, as discussed below.
The atm potential is typically used in combination with a two-body potential using the pair_style hybrid/overlay command as in the example above.
The potential for a triplet of atom is calculated only if all 3 distances \(r_{12}\), \(r_{23}\), \(r_{31}\) between the three atoms satisfy \(r_{IJ} < \text{cutoff}\). In addition, the product of the 3 distances \(r_{12} r_{23} r_{31}\) < cutoff_triple \(^3\) is required, which excludes from calculation the triplets with small contribution to the interaction.
The following coefficients must be defined for each pair of atoms types via the pair_coeff command as in the examples above, or in the restart files read by the read_restart commands:
\(K\) = atom type of the third atom (1 to \(N_{\text{types}}\))
\(\nu\) = prefactor (energy/distance^9 units)
\(K\) can be specified in one of two ways. An explicit numeric value or type label can be used, as in the second example above. LAMMPS sets the coefficients for the other 5 symmetric interactions to the same values. E.g. if \(I = 1\), \(J = 2\), \(K = 3\), then these 6 values are set to the specified \(\nu\): \(\nu_{123}\), \(\nu_{132}\), \(\nu_{213}\), \(\nu_{231}\), \(\nu_{312}\), \(\nu_{321}\). This enforces the symmetry discussed above.
A wildcard asterisk can be used for K to set the coefficients for multiple triplets of atom types. This takes the form “*” or “*n” or “n*” or “m*n”. If \(N\) equals the number of atom types, then an asterisk with no numeric values means all types from 1 to \(N\). A leading asterisk means all types from 1 to \(n\) (inclusive). A trailing asterisk means all types from \(n\) to \(N\) (inclusive). A middle asterisk means all types from \(m\) to \(n\) (inclusive). Note that only type triplets with \(J \leq K\) are considered; if asterisks imply type triplets where \(K < J\), they are ignored.
Note that a pair_coeff command can override a previous setting for the same \(I,J,K\) triplet. For example, these commands set \(\nu\) for all \(I,J.K\) triplets, then overwrite nu for just the \(I,J,K = 2,3,4\) triplet:
pair_coeff * * * 0.25
pair_coeff 2 3 4 0.1
Note that for a simulation with a single atom type, only a single entry is required, e.g.
pair_coeff 1 1 1 0.25
For a simulation with two atom types, four pair_coeff commands will specify all possible nu values:
pair_coeff 1 1 1 nu1
pair_coeff 1 1 2 nu2
pair_coeff 1 2 2 nu3
pair_coeff 2 2 2 nu4
For a simulation with three atom types, ten pair_coeff commands will specify all possible nu values:
pair_coeff 1 1 1 nu1
pair_coeff 1 1 2 nu2
pair_coeff 1 1 3 nu3
pair_coeff 1 2 2 nu4
pair_coeff 1 2 3 nu5
pair_coeff 1 3 3 nu6
pair_coeff 2 2 2 nu7
pair_coeff 2 2 3 nu8
pair_coeff 2 3 3 nu9
pair_coeff 3 3 3 nu10
By default the \(\nu\) value for all triplets is set to 0.0. Thus it is not required to provide pair_coeff commands that enumerate triplet interactions for all \(K\) types. If some \(I,J,K\) combination is not specified, then there will be no 3-body ATM interactions for that combination and all its permutations. However, as with all pair styles, it is required to specify a pair_coeff command for all \(I,J\) combinations, else an error will result.
Mixing, shift, table, tail correction, restart, rRESPA info
This pair style do not support the pair_modify mix, shift, table, and tail options.
This pair style writes its information to binary restart files, so pair_style and pair_coeff commands do not need to be specified in an input script that reads a restart file. However, if the atm potential is used in combination with other potentials using the pair_style hybrid/overlay command then pair_coeff commands need to be re-specified in the restart input script.
This pair style can only be used via the pair keyword of the run_style respa command. It does not support the inner, middle, and outer keywords.
Restrictions
This pair style is part of the MANYBODY package. It is only enabled if LAMMPS was built with that package. See the Build package page for more info.
Default
none
(Axilrod) Axilrod and Teller, J Chem Phys, 11, 299 (1943); Muto, Nippon Sugaku-Buturigakkwaishi 17, 629 (1943).