\(\renewcommand{\AA}{\text{Å}}\)
pair_style hbond/dreiding/lj command
Accelerator Variants: hbond/dreiding/lj/omp
pair_style hbond/dreiding/lj/angleoffset command
Accelerator Variants: hbond/dreiding/lj/angleoffset/omp
pair_style hbond/dreiding/morse command
Accelerator Variants: hbond/dreiding/morse/omp
pair_style hbond/dreiding/morse/angleoffset command
Accelerator Variants: hbond/dreiding/morse/angleoffset/omp
Syntax
pair_style style N inner_distance_cutoff outer_distance_cutoff angle_cutoff equilibrium_angle
style = hbond/dreiding/lj or hbond/dreiding/morse or hbond/dreiding/lj/angleoffset or hbond/dreiding/morse/angleoffset
N = power of cosine of angle theta (integer)
inner_distance_cutoff = global inner cutoff for Donor-Acceptor interactions (distance units)
outer_distance_cutoff = global cutoff for Donor-Acceptor interactions (distance units)
angle_cutoff = global angle cutoff for Acceptor-Hydrogen-Donor interactions (degrees)
(with style angleoffset) equilibrium_angle = global equilibrium angle for Acceptor-Hydrogen-Donor interactions (degrees)
Examples
pair_style hybrid/overlay lj/cut 10.0 hbond/dreiding/lj 4 9.0 11.0 90.0
pair_coeff 1 2 hbond/dreiding/lj 3 i 9.5 2.75 4 9.0 11.0 90.0
pair_style hybrid/overlay lj/cut 10.0 hbond/dreiding/morse 2 9.0 11.0 90.0
pair_coeff 1 2 hbond/dreiding/morse 3 i 3.88 1.7241379 2.9 2 9.0 11.0 90.0
labelmap atom 1 C 2 O 3 H
pair_coeff C O hbond/dreiding/morse H i 3.88 1.7241379 2.9 2 9.0 11.0 90.0
pair_style hybrid/overlay lj/cut 10.0 hbond/dreiding/lj 4 9.0 11.0 90 170.0
pair_coeff 1 2 hbond/dreiding/lj 3 i 9.5 2.75 4 9.0 11.0 90.0
Description
The hbond/dreiding styles compute the Acceptor-Hydrogen-Donor (AHD) 3-body hydrogen bond interaction for the DREIDING force field, given by:
where \(r_\mathrm{in}\) is the inner spline distance cutoff, \(r_\mathrm{out}\) is the outer distance cutoff, \(\theta_c\) is the angle cutoff, and \(n\) is the power of the cosine of the angle \(\theta\).
Here, r is the radial distance between the donor (D) and acceptor (A) atoms and \(\theta\) is the bond angle between the acceptor, the hydrogen (H) and the donor atoms:
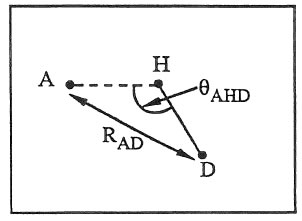
These 3-body interactions can be defined for pairs of acceptor and donor atoms, based on atom types. For each donor/acceptor atom pair, the third atom in the interaction is a hydrogen permanently bonded to the donor atom, e.g. in a bond list read in from a data file via the read_data command. The atom types of possible hydrogen atoms for each donor/acceptor type pair are specified by the pair_coeff command (see below).
Style hbond/dreiding/lj is the original DREIDING potential of (Mayo). It uses a LJ 12/10 functional for the Donor-Acceptor interactions. To match the results in the original paper, use n = 4.
Style hbond/dreiding/morse is an improved version using a Morse potential for the Donor-Acceptor interactions. (Liu) showed that the Morse form gives improved results for Dendrimer simulations, when n = 2.
Added in version 4Feb2025.
The style variants hbond/dreiding/lj/angleoffset and hbond/dreiding/lj/angleoffset take the equilibrium angle of the AHD as input, allowing it to reach 180 degrees. This variant option was added to account for cases (especially in some coarse-grained models) in which the equilibrium state of the bonds may equal the minimum energy state.
See the Howto bioFF page for more information on the DREIDING force field.
Note
Because the Dreiding hydrogen bond potential is only one portion of an overall force field which typically includes other pairwise interactions, it is common to use it as a sub-style in a pair_style hybrid/overlay command, where another pair style provides the repulsive core interaction between pairs of atoms, e.g. a 1/r^12 Lennard-Jones repulsion.
Note
When using the hbond/dreiding pair styles with pair_style hybrid/overlay, you should explicitly define pair interactions between the donor atom and acceptor atoms, (as well as between these atoms and ALL other atoms in your system). Whenever pair_style hybrid/overlay is used, ordinary mixing rules are not applied to atoms like the donor and acceptor atoms because they are typically referenced in multiple pair styles. Neglecting to do this can cause difficult-to-detect physics problems.
Note
In the original Dreiding force field paper 1-4 non-bonded interactions ARE allowed. If this is desired for your model, use the special_bonds command (e.g. “special_bonds lj 0.0 0.0 1.0”) to turn these interactions on.
Note
For the angleoffset variants, the referenced angle offset is the supplementary angle of the equilibrium angle parameter. It means if the equilibrium angle is 166.6 degrees, the calculated angle offset is 13.4 degrees.
The following coefficients must be defined for pairs of eligible donor/acceptor types via the pair_coeff command as in the examples above.
Note
Unlike other pair styles and their associated pair_coeff commands, you do not need to specify pair_coeff settings for all possible I,J type pairs. Only I,J type pairs for atoms which act as joint donors/acceptors need to be specified; all other type pairs are assumed to be inactive.
Note
A pair_coeff command can be specified multiple times for the same donor/acceptor type pair. This enables multiple hydrogen types to be assigned to the same donor/acceptor type pair. For other pair_styles, if the pair_coeff command is re-used for the same I.J type pair, the settings for that type pair are overwritten. For the hydrogen bond potentials this is not the case; the settings are cumulative. This means the only way to turn off a previous setting, is to re-use the pair_style command and start over.
For the hbond/dreiding/lj style the list of coefficients is as follows:
K = hydrogen atom type = 1 to Ntypes, or type label
donor flag = i or j
\(\epsilon\) (energy units)
\(\sigma\) (distance units)
n = exponent in formula above
distance cutoff \(r_\mathrm{in}\) (distance units)
distance cutoff \(r_\mathrm{out}\) (distance units)
angle cutoff (degrees)
For the hbond/dreiding/morse style the list of coefficients is as follows:
K = hydrogen atom type = 1 to Ntypes, or type label
donor flag = i or j
\(D_0\) (energy units)
\(\alpha\) (1/distance units)
\(r_0\) (distance units)
n = exponent in formula above
distance cutoff \(r_\mathrm{in}\) (distance units)
distance cutoff \(r_{out}\) (distance units)
angle cutoff (degrees)
For both the hbond/dreiding/lj/angleoffset and hbond/dreiding/morse/angleoffset styles an additional parameter is added: * equilibrium angle (degrees)
For all styles, a single hydrogen atom type K can be specified, or a wild-card asterisk can be used in place of or in conjunction with the K arguments to select multiple types as hydrogen atoms. This takes the form “*” or “*n” or “n*” or “m*n”. See the pair_coeff command page for details.
If the donor flag is i, then the atom of type I in the pair_coeff command is treated as the donor, and J is the acceptor. If the donor flag is j, then the atom of type J in the pair_coeff command is treated as the donor and I is the donor. This option is required because the pair_coeff command requires that I <= J.
\(\epsilon\) and \(\sigma\) are settings for the hydrogen bond potential based on a Lennard-Jones functional form. Note that sigma is defined as the zero-crossing distance for the potential, not as the energy minimum at \(2^{1/6} \sigma\).
\(D_0\) and \(\alpha\) and \(r_0\) are settings for the hydrogen bond potential based on a Morse functional form.
The last 3 coefficients for both styles are optional. If not specified, the global n, distance cutoff, and angle cutoff specified in the pair_style command are used. If you wish to only override the second or third optional parameter, you must also specify the preceding optional parameters.
Styles with a gpu, intel, kk, omp, or opt suffix are functionally the same as the corresponding style without the suffix. They have been optimized to run faster, depending on your available hardware, as discussed on the Accelerator packages page. The accelerated styles take the same arguments and should produce the same results, except for round-off and precision issues.
These accelerated styles are part of the GPU, INTEL, KOKKOS, OPENMP, and OPT packages, respectively. They are only enabled if LAMMPS was built with those packages. See the Build package page for more info.
You can specify the accelerated styles explicitly in your input script by including their suffix, or you can use the -suffix command-line switch when you invoke LAMMPS, or you can use the suffix command in your input script.
See the Accelerator packages page for more instructions on how to use the accelerated styles effectively.
Mixing, shift, table, tail correction, restart, rRESPA info
These pair styles do not support mixing. You must explicitly identify each donor/acceptor type pair.
These styles do not support the pair_modify shift option for the energy of the interactions.
The pair_modify table option is not relevant for these pair styles.
These pair styles do not support the pair_modify tail option for adding long-range tail corrections to energy and pressure.
These pair styles do not write their information to binary restart files, so pair_style and pair_coeff commands need to be re-specified in an input script that reads a restart file.
These pair styles can only be used via the pair keyword of the run_style respa command. They do not support the inner, middle, outer keywords.
These pair styles tally a count of how many hydrogen bonding interactions they calculate each timestep and the hbond energy. These quantities can be accessed via the compute pair command as a vector of values of length 2.
To print these quantities to the log file (with a descriptive column heading) the following commands could be included in an input script:
compute hb all pair hbond/dreiding/lj
variable n_hbond equal c_hb[1] #number hbonds
variable E_hbond equal c_hb[2] #hbond energy
thermo_style custom step temp epair v_E_hbond
Restrictions
The base pair styles can only be used if LAMMPS was built with the MOLECULE package. The angleoffset variant also requires the EXTRA-MOLECULE package. See the Build package doc page for more info.
Default
none
(Mayo) Mayo, Olfason, Goddard III, J Phys Chem, 94, 8897-8909 (1990).
(Liu) Liu, Bryantsev, Diallo, Goddard III, J. Am. Chem. Soc 131 (8) 2798 (2009)